
우연히 들렀던 인터넷의 독서카페에서 발견한 이공계 대학생의 필독서라고 하는 이 책...18세기의 수학자 페르마가 피타고라스의 정리를 응용한 공식을 자신은 증명했지만 책의 여백이 없어서 남겨놓지 못했다고 하는 오만한 기록을 정리한 책이다.
페르마의 마지막 정리를 설명하면 이렇다.
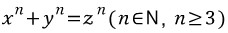 을 만족하는 정수 (x, y, z)의 순서쌍은 존재하지 않는다...
을 만족하는 정수 (x, y, z)의 순서쌍은 존재하지 않는다...
이 책에는 위의 공식을 증명하기 위해서 자신의 정열을 바친 수학자들의 이야기가 나온다. 뛰어난 능력을 보유한 수학자라면 한번쯤은 도전한 과제였고 일부는 증명의 해를 풀어낸 사람도 있다. 페르마가 제시했던 몇가지의 논제들은 대부분 증명되었지만 마지막 정리 하나는 최종적인 증명이 나오기까지 300년동안 많은 수학자들을 힘들게 했다. 그러나 수많은 수학자들이 조금씩 내놓았던 해결방안들을 잘 활용하여 최종적으로 프린스턴대학교의 앤드루 와일즈 교수가 1995년에 증명하게 된다. 컴퓨터가 발달한 최근에는 수학적인 증명방법에 의한 방식 말고도 컴퓨터를 활용해서 해를 구하는 시도들을 하고 있는데 이를 만족하는 (x,y,z) 쌍은 아직까지 발견되지 않았다고 한다. 앤드루 와일즈 교수의 증명이 틀리지 않았다면 당연한 것이다. 그렇지만 수학적 사실증명에 재미를 가진 사람이라면 한번쯤 프로그램을 돌려보고 싶은 충동이 들 것이다. 내가 알고 있는 몇몇 친구들처럼 말이다.
대학시절 2년이나 배워야 했던 공업수학을 제대로 소화하지 못해서 참 힘들었는데 그 이유를 이제야 알게 되었다. 난 고교시절 수학을 제대로 이해한 것이 아니었다. 수학정석을 몇번씩 풀어보았고 과외선생도 했었는데 "페르마의 마지막 정리"에 실린 수학의 원리들을 보고 수학이 무엇인지 깨닫게 되었으니 말이다.
학창시절 수학이 어려웠던 분이라면 이 책을 한번 읽어보시라고 권하고 싶다. 하지만 이 책은 읽는 방법을 잘 지켜야 한다. 스킵 & 스캐닝이라고 하는 독서 방법이다. 여기에 나오는 수학풀이들은 내용을 이해하기 어렵다. 이걸 하나하나 다 읽으려고 하면 책읽기를 포기하게 된다. 그러므로 스킵 & 스캐닝 읽기 방법은 어려운 부분은 스킵하고 이해할 수 있는 쉬운 부분만 잘 읽어나가는 방법이다. 그러다가 관심있는 부분이 보이면 집중하여 보면 된다. 물론 이런 책 읽기 방법도 연습이 필요하다.
오늘(6.28) 인터넷 기사에 의하면 일단의 수학자들이 새로운 용어의 사용을 주장하고 있다. 세 변의 세제곱 이상에 대한 정리를 원주율, 즉 원주의 길이와 그 지름의 비율을 나타내는 '파이(π)'는 소수점 아래 무한대로 내려가는, 수학에서 가장 중요하고 유명한 상수 중 하나다. 그런데 이것이 잘못 되었다며 모든 학교 수학교과서에 있는 파이는 타우(τ)로 대체돼야 한다는 게 이들의 견해다. 타우의 대략적인 값은 6.28로 파이(3.14)의 2배 이다.
파이는 수학과 과학, 공학의 여러 공식에서 근간이 되는 상수이다. 그래서 많은 곳에서 활용되고 있는데 파이(π)보다는 2π가 더 많이 쓰이고 있다는 것이다. 예를 들면 원의 둘레는 2πr인것이고 각도 표시에 있어서 360도를 2π라디안으로 계산하는 것처럼 2π를 쓰는 것이 훨씬 자연스럽다고 휴스턴 박사등이 주장하고 있다. 2π가 바로 타우(τ)라고 표시된다. 파이(π)의 두배인 6.28을 원과 관련한 자연 상수로 사용하자는 제안은 미국 유타대의 밥 팰레이 박사에 의해 처음 제기됐고 미국의 다른 수학자 마이클 하틀 박사가 이를 그리스 문자 'π'와 비슷한 모양의 'τ'로 표기할 것을 주창했다.
이것을 이해하고 활용하는 것이 쉬운 일은 아니다. 우리가 그동안 자연스럽게 수학시간에 파이(π)를 배워왔는데 어느날 갑자기 타우(τ)라고 하는 새로운 기호를 익혀야 한다니 말이다. 이들이 주장하길 야드법을 미터법으로 바꾸는 것보다는 쉬우며 어린이부터 가르치면 된다고 한다.
어쨌든 그리스의 탈레스 이후 오랜시간에 걸쳐서 발전시켜왔고 우리 생활에 보이지 않게 영향력을 미쳐온 수학이라는 존재에 대해서 이해하고 관심가질만한 책을 읽어보는 것도 나름 의미가 있다. 경제학의 가장 기초적인 이해는 수학에서 출발하니 말이다.
*** 오늘의 독서경영, 핵심메시지 ***
1. 수학에서는 증명되지 않는 것은 정확한 사실이 아니다. 수학에서처럼 명확하게 논리적으로 세상을 풀어보고 이해할 수 있는 능력을 키우는 것...이것을 수학을 배우는 목적이다.
2. 파이의 의미를 아는가? 허수는 왜 생겼으며 어떤 때 쓰일까? 이것들은 책에서만 존재하는 것이 아니다. 바로 우리 곁에 있다. 공학자가 만든 건물에, 제품에 다 숨어있다.
3. 어려운 책을 읽어나가는 방법 "스킵 & 스캐닝" 어려운 부분은 스킵하고, 쉬운부분은 자세히 읽는 방법...꼭 읽고 싶은데 포기하지 않고 끝까지 읽어낼 수 있는 독서법
오늘의 독서경영
안계환 드림
'2011년' 카테고리의 다른 글
| 7월 20일 40라운드 정기모임은 개최하지 않기로 협의 했습니다! (0) | 2011.07.18 |
|---|---|
| [최카피의 카피여행]프리허그 (3) | 2011.07.18 |
| 2011년 제7회 40라운드 정기모임 공지 (8) | 2011.07.14 |
| 1018 청소년을 위한 나를 찾아 떠나는 여행, 드림캠프! (10) | 2011.07.10 |
| 공식행사> 40라운드 정체성을 위한 소통의 밤! (10) | 2011.06.30 |
| 모두에 감사하고 귀기울여라.by포토테라피스트 백승휴 (6) | 2011.06.24 |
| 울릉도는 사진가만 다녀온게 아니다. (7) | 2011.06.23 |
| 청소년을 위한 나를 찾아 떠나는 여행 '드림캠프' (10) | 2011.06.21 |
| 포토에세이과정의 종강을 하며.. by 포토테라피스트 백승휴 (9) | 2011.06.19 |
| 채선당과 함께하는 주부공개오디션 Miss 변신 프로젝트 with 포토테라피스트 백승휴, 지식소통 조연심 (9) | 2011.06.19 |